
カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
Q円すい側面の扇形の中心角と底面の半径がわかっているときの母線の求め方 円すいの中心角と底面の円の半径がわかっている状態から その円すいの母線の長さを求めるにはどうしたら良いでしょうか。 自分で考えてみましたがどうしても答えにありつけ 側面である扇形の面積を求めようとすると、扇形の公式から分かるように 中心角が必要になります。 というわけで、 まずは扇形の中心角を求めていきます。 底面の円周の長さと側面の弧の長さが等しいことを利用すると
扇形 中心角 求め方 母線
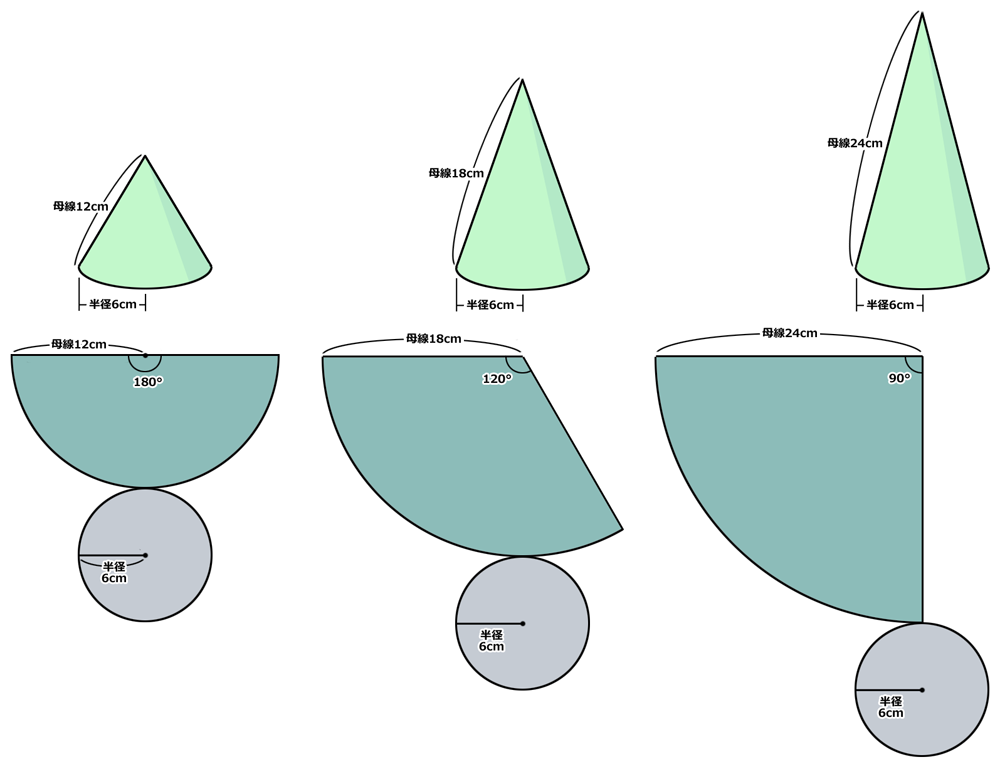
扇形 中心角 求め方 母線- 扇形の面積 = 底面の円の面積 + 扇形の面積 = R × R × π + ( L × L × π ) × 2Rπ / 2Lπ = R2 π + LRπ これで、扇形の表面積を計算することができました。 毎回このように計算してももちろんよいのですが、この計算結果から1つの公式を求めることができ側面の「扇形の中心角」を求める つぎは円錐の側面の展開図をかくためのステップだ。 ここでは、円錐の側面を展開したときにできる「扇形の中心角」を求めるんだ! Step1で「底面の円周の長さ」を求めたよね? ? じつは、円錐の展開図ではソレが「 扇形の弧の長さ 」になっているんだ。

この扇形の中心角の求め方が分かりません 解説お願いします Clearnote
中心角の求め方です。 扇形の弧の部分と、底面の円の円周は同じ寸法です。 中心角=半径÷母線×360 扇形の中心角 円の面積は、半径×半径×314で求められます。 扇形の面積は、母線×母線×314×(中心角÷360)です。 扇形の中心角を求める公式は、 x = 180 × 弧の長さ π × 半径 x = 180 × 弧 の 長 さ π × 半 径 弧の長さ= L、半径= r とすると、 x = 180L πr x = 180 L π r だよ 公式は忘れちゃったら解けないし、これを覚えるのは大変だよ だから、きっちり 本質 を理解しようね具体例で学ぶ数学 > 図形 > 円錐の母線、半径、中心角の関係式とそれぞれの求め方 最終更新日 r = l × x 360 という式を使うことで、 母線の長さ l 、 底面の半径 r 、 側面のおうぎ形の中心角 x のうち2つが分かれば残りの1つを計算できる。 なお
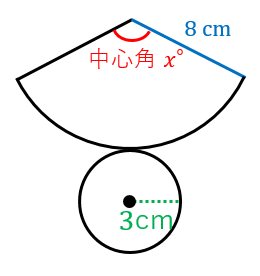
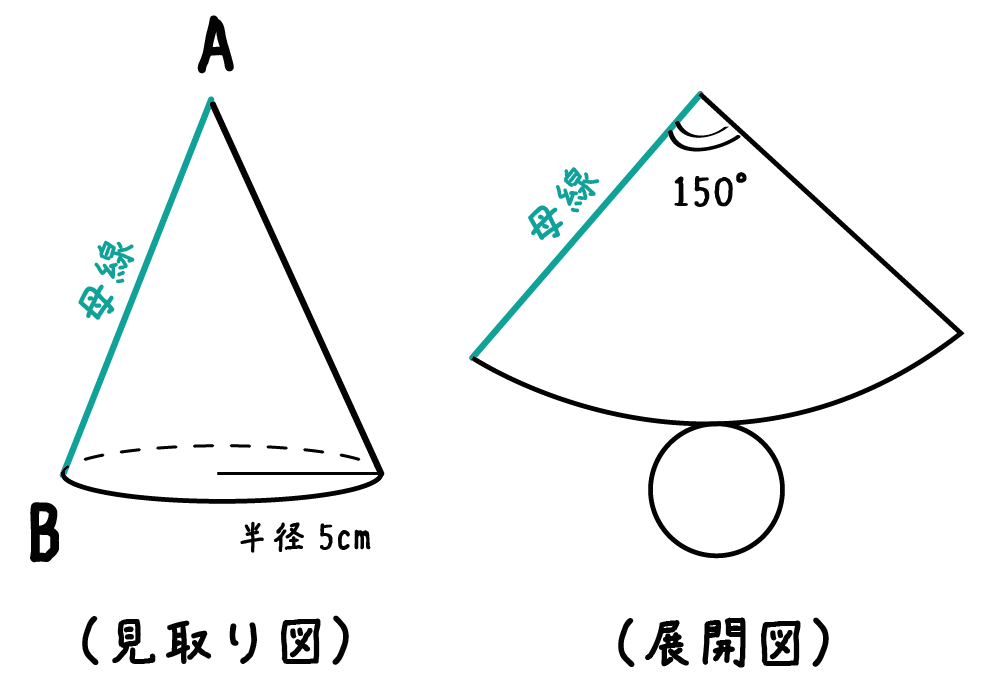
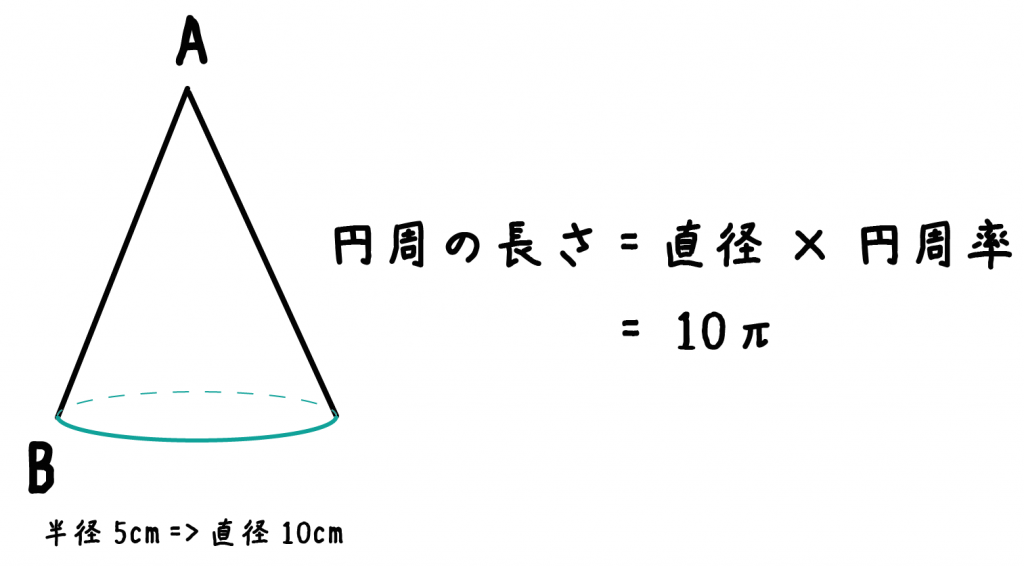
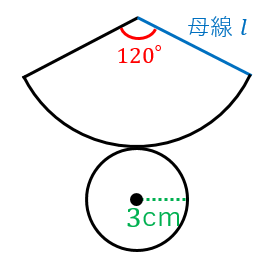
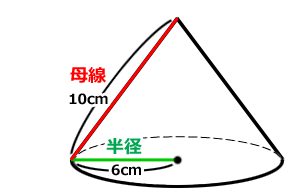
楽しい数学:『中心角の裏ワザ』 『 底面の半径3cm、母線の長さ5cmの円すいの側面のおうぎ形の中心角を求めなさい。 』 この問題も円すいを展開図にしてから考えます。 展開図にすると、オレンジの部分が側面、白い円が底面になります。 つまり 扇形の中心角の求め方の公式を知りたい! こんにちは、この記事をかいているKenだよー!豆乳ラテだったら3杯はいけるね。 「扇形の中心角の求め方」の公式 ってチョー便利。 教科書にはのっていない「知る人ぞ知る公式」なんだ。カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも 中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわ
扇形 中心角 求め方 母線のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「扇形 中心角 求め方 母線」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「扇形 中心角 求め方 母線」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「扇形 中心角 求め方 母線」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「扇形 中心角 求め方 母線」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「扇形 中心角 求め方 母線」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「扇形 中心角 求め方 母線」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「扇形 中心角 求め方 母線」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「扇形 中心角 求め方 母線」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「扇形 中心角 求め方 母線」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「扇形 中心角 求め方 母線」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「扇形 中心角 求め方 母線」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
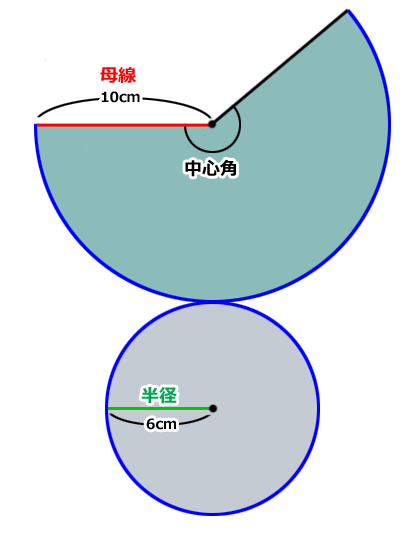 |
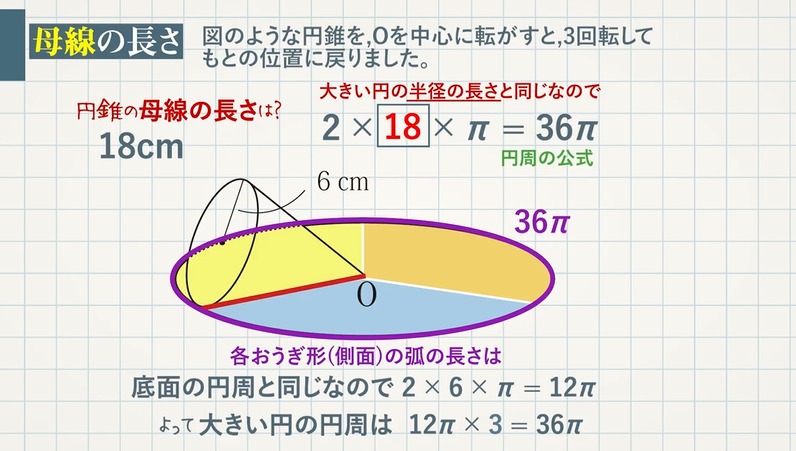
問題図のような円錐を、Oを中心に転がすと、 $\textcolor{green}{3}$ 回転してもとの位置に戻りました。 円錐の母線の長さを求めなさい。 $3$ 回転ということは、中心がOである 大きい円の円周 は、 側面のおうぎ形 $\textcolor{blue}{3}$ 枚分の長さ と等しくなります。 扇型の求め方や中心角の求め方も分からないので 解説もお願いします😓 この問題の答えは 『27π』になります (0 右の図は底面の半径が 3 cm で, 母線の長さが 6 cm の円すいである。 この円すいの表面積は cm' である。 ただし, 円周率はヵと する。 中2





0 件のコメント:
コメントを投稿